A máquina de estados finita em sistemas digitais, quando realizada na forma de um circuito digital, utiliza recursos computacionais (e.g. flip-flops, memórias, portas lógicas, etc.) que são caros do ponto de vista de área e consumo de energia, principalmente se a máquina possuir muitos estados. Por este motivo, é importante minimizar o número de estados da máquina para que, na implementação, utilizemos somente os recursos mínimos necessários para aquela máquina. Além disso, quando estamos projetando uma máquina de estados para resolver um problema, é mais confortável não pensar em otimizações mas sim na funcionalidade da máquina, para só depois pensar na otimização. De fato, a maioria dos projetistas comerciais não pensa na otimização quando estão modelando o problema pois isso nem sempre é possível (i.e. o projetista não tem visão da máquina toda mas sim da parte cabível a ele, a máquina é muito grande tornando impossível pensar em tudo, a máquina é particionada, etc).

Na prática, com os sintetizadores modernos, você pode especificar sua máquina usando a linguagem de descrição de hardware de sua preferência e deixar o sintetizador otimizá-la para você. Os resultados da otimização automática são bons quando comparados aos métodos manuais [1,2]. Contudo, é necessário conhecer o mínimo do funcionamento dos algoritmos de minimização pois, quando for descrever sua máquina, você conhecerá ao menos o básico do que acontecerá quando sintetizá-la. Neste artigo, explicarei os métodos de minimização por identificação direta na tabela de transição de estados e por tabela de implicação. Em ambos os casos, o objetivo principal é encontrar estados equivalentes, ou seja, que para a mesma entrada, produzem a mesma saída e transicionam para os mesmos estados.

Minimização através da tabela de transição

Em muitos casos, é fácil identificar os estados equivalentes na tabela de transição de estados, por isso este método também é chamado de observação direta ou casamento de linhas. O algoritmo é simples:

1. Elimine todos os estados inalcançáveis (estados onde não chega nenhuma aresta partindo de outro estado alcançável).
2. Identifique dois estados A e B que, para a mesma entrada, produzam exatamente a mesma saída e realizem a mesma transição (transicionem para o mesmo estado).
3. Elimine um dos estados (e.g. B) apagando a linha correspondente a este estado e substitua todas as ocorrências de B por A (i.e. todos as transições para B agora devem apontar para A).
4. Repita até que nenhum par de estados atenda (2).

Exemplo

Uma forma muito comum de projetar máquinas de estados é modelando-a como árvore, onde cada ramificação é uma tomada de decisão. Tomemos a máquina abstrata a seguir que foi montada partindo de uma árvore binária canônica e modificada para reconhecer as sequencias 0011 e 1001:

Em vermelho está destacado o caminho que esta máquina irá seguir para reconhecer as duas sequencias. Note que esta é uma máquina de Mealy e não leva em consideração nenhuma sobreposição entre as sequencias detectadas, ou seja, ela só funciona para entradas de 4 bits agrupados a partir do reset (e.g. detecta duas vezes se a entrada for 0011 1001 mas não detecta a segunda vez se a entrada for 0011 001).

A tabela de transição de estados fica como na Tabela 1 a seguir.

Tabela 1
E.A.	P.E.
	0	1
S0	S1/0	S2/0
S1	S3/0	S4/0
S2	S5/0	S6/0
S3	S7/0	S8/0
S4	S9/0	S10/0
S5	S11/0	S12/0
S6	S13/0	S14/0
S7	S0/0	S0/0
S8	S0/0	S0/1
S9	S0/0	S0/0
S10	S0/0	S0/0
S11	S0/0	S0/1
S12	S0/0	S0/0
S13	S0/0	S0/0
S14	S0/0	S0/0

Tabela 2
E.A.	P.E.
	0	1
S0	S1/0	S2/0
S1	S3/0	S4/0
S2	S5/0	S6/0
S3	Sa/0	S8/0
S4	Sa/0	Sa/0
S5	S11/0	Sa/0
S6	Sa/0	Sa/0
S8	S0/0	S0/1
S11	S0/0	S0/1
Sa	S0/0	S0/0

Tabela 3
E.A.	P.E.
	0	1
S0	S1/0	S2/0
S1	S3/0	Sb/0
S2	S5/0	Sb/0
S3	Sa/0	Sc/0
S5	Sc/0	Sa/0
Sb	Sa/0	Sa/0
Sc	S0/0	S0/1
Sa	S0/0	S0/0

A coluna E.A. mostra o estado atual, e a coluna P.E. o próximo estado. Esta última é bipartida para as entradas igual a 0 e igual a 1.

A Tabela 1 possui todas as transições da árvore como vista na figura. Esta máquina não tem nenhum estado inalcançável, então não há o que eliminar no passo 1.

No passo 2, devemos procurar as equivalências. É fácil perceber que há estados que produzem exatamente o mesmo resultado (transição e saída) para determinada entrada. Tomemos por exemplo os estados S7, S9, S10, S12, S13 e S14: todos transicionam para S0 e produzem saída 0 para qualquer entrada, portanto são equivalentes. Podemos reduzir a tabela substituindo todos estes estados por um estado Sa, o que podemos ver na Tabela 2, destacado em verde.

Se fizermos a busca novamente, os estados S4 e S6 agora são equivalentes pois ambos transicionam para Sa e produzem saída 0, independententemente da entrada. Criamos o estado Sb, em vermelho, para substituir estes estados. Similarmente os estados S8 e S11 são equivalentes, mas note que eles tem saídas diferentes para entradas diferentes. Para este conjunto de estados, criamos Sc, em amarelo. Não há mais estados equivalentes e o resultado final pode ser visto na Tabela 3.

O diagrama de transição de estados minimizado pode ser visto na figura ao lado. Os estados S7, S9, S10, S12, S13 e S14 são representados pelo Sa, S4 e S6 pelo Sb e S8 e S11 pelo Sc.

O método de análise da tabela de transição de estados se baseia na busca exaustiva por estados equivalentes. É fácil perceber que, conforme a tabela cresce, ficará mais difícil visualizar os estados equivalentes. Além disso, o método não garante a menor quantidade de estados possível pois é baseado em estados e não em grupos de estados (veja o primeiro exemplo da próxima seção).

O método de minimização por tabela de implicação

Nem sempre é tão fácil perceber a equivalência de estados através da tabela de transição de estados, especialmente para máquinas grandes ou com muitas entradas. No entanto, os projetistas desenvolveram um método chamado de tabela de implicação. Este método é equivalente à análise através da tabela de transição de estados, porém é algorítmico e está organizado em forma de uma matriz, o que minimiza erros por parte do projetista. Além disso, apesar de ambos os métodos serem exaustivos, há uma diferença primordial: enquanto o método de análise da tabela de transição de estados procura exaustivamente estados equivalentes, o método da tabela de implicação procura exaustivamente os estados que não são equivalentes. Parte-se da premissa de que todos os estados são equivalentes entre si e, a cada iteração, elimina-se os estados que não podem ser equivalentes. Os estados que sobrarem são equivalentes.

Há dois momentos no método da tabela de implicação: a construção da tabela e a análise.

Construção da matriz (tabela)

A matriz pode ser construída como uma matriz $n$ por $n$, onde $n$ é o número de estados (se você começar no $S_0$, o último estado será $S_{n-1}$). Cada linha $i$ da matriz representa um estado e cada coluna $j$ também.

Não faz sentido analisar a equivalência de um estado com ele mesmo, pois um estado sempre é equivalente a ele mesmo. Por este motivo, eliminamos a diagonal da matriz, onde $i=j$. As metades diagonais superiores e inferiores significam a mesma coisa pois se uma célula $X_{ij}$ mostra equivalência entre o estado $S_i$ e o estado $S_j$, a célula $X_{ji}$ também deve mostrar a mesma equivalência. Por este motivo, eliminamos também uma das metades diagonais. Por convenção, elimina-se a diagonal superior, mas o resultado é o mesmo se você eliminar a metade diagonal inferior.

Quando estiver confortável com a construção da matriz, você poderá desenhá-la já sem a diagonal e sem a metade diagonal superior. A esse desenho contendo somente a metade diagonal inferior da tabela, chamamos de tabela de implicação. Na figura abaixo mostramos a matriz inteira, a matriz destacando a linha diagonal (vermelha) e a metade diagonal superior (laranja), e finalmente a tabela de implicação.

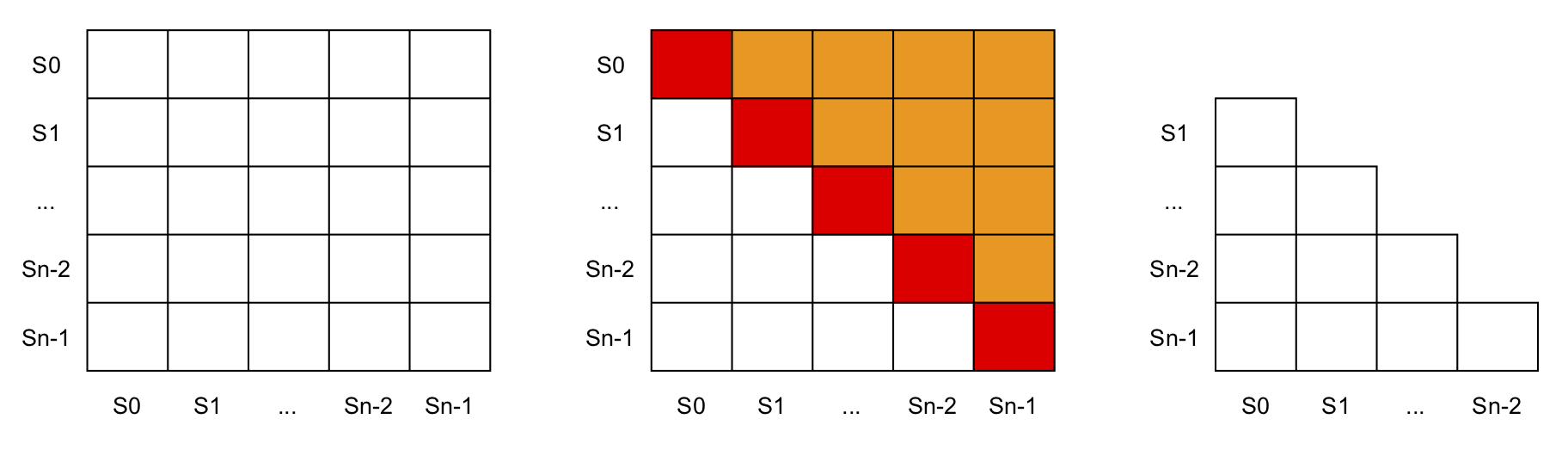
Após obter a tabela de implicação, devemos preencher as células. Cada célula terá $2^b$ linhas, onde $b$ é o número de bits da entrada. E.g. se a entrada for de 1 bit, cada célula tem 2 linhas; se a entrada for de 2 bits, cada célula tem 4 linhas. Cada linha da entrada corresponde às transições daqueles estados para aquela entrada.

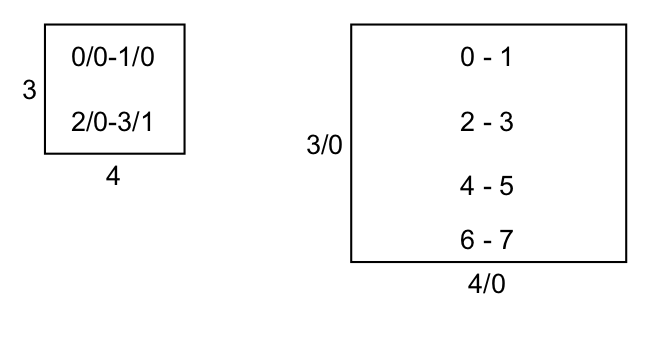Na figura podemos ver o exemplo do preenchimento para duas células, ambas na linha do S3 e coluna do S4. Para simplificar o preenchimento, usamos somente o número do estado, mas você pode escrever o nome completo do estado (especialmente útil se os nomes dos estados não forem numerados).

Na célula na esquerda na figura, a entrada tem 1 bit, portanto temos duas linhas, uma para a entrada 0 e outra para a entrada 1. Nesta célula, a máquina é de Mealy com saída de 1 bit, que pode ser vista representada nas transições.

Já na célula a direita na figura, a entrada tem 2 bits, portanto temos 4 linhas para as entradas 00, 01, 10 e 11. A máquina representada é de Moore e também tem um bit só de saída, que nesse caso é representado no estado e não na transição.

Os números em cada linha correspondem a transição que o estado fará para cada entrada (e à saída referente àquela transição no caso de uma máquina de Mealy). No exemplo a esquerda na figura, podemos assumir que, para uma determinada entrada e estando em S3 ou em S4, a máquina transicionará para o estado S0/0 ou S1/0 (note que em ambas as transições a saída é 0). Na mesma situação mas para a outra entrada, a máquina transicionará para o estado S2/0 ou S3/1. Mas como eu sei qual entrada? Não é preciso saber para qual entrada, apenas que as transições da mesma linha, separadas por -, são para a mesma entrada. De fato, alguns projetistas preferem ordenar as transições em ordem crescente para facilitar a busca por estados equivalentes. E.g. (linha superior / linha inferior) 3-2/1-2 é o mesmo que 1-2/2-3, mas ordenado. Fica a seu critério decidir a melhor forma de organizar sua tabela de implicação, mas lembre-se que cada linha corresponde a exatamente dois estados separados por -, para os quais a máquina de estados transicionará quando houver a mesma entrada.

É de praxe também assinalar os estados que produzem saídas diferentes, pois eles não podem ser equivalentes. Neste caso, coloque uma / no índice de coluna e linha (caso a máquina for de Moore) ou na transição dentro da célula (caso a máquina for de Mealy). Isto ficará mais claro no exemplo.

Procurando estados equivalentes

Com a tabela de implicação construída, devemos procurar os estados equivalentes. Isto é feito de forma exaustiva, analisando todas as células da tabela.

1. Risque todas as transições que vão para o mesmo estado e produzem a mesma saída (tipo s-s), pois elas são naturalmente equivalentes. E.g. se você tem uma transição 0-0, risque-a pois não é preciso analisá-la.
2. Elimine as células com estados (Moore) ou transições (Mealy) que produzem saídas diferentes. Estes estados nunca poderão ser equivalentes.
3. Analise uma célula qualquer que não tenha todas as transições riscadas e que não tenha sido eliminada anteriormente. Esta célula é uma candidata a equivalência.
   • Olhe todas as linhas da célula que não foram riscadas no passo (1). Para cada uma, analise a célula alvo. E.g. se a transição marca 1-2, você deve analisar a célula correspondente aos estados S1 e S2.
   • Se a célula alvo estiver eliminada, você deve eliminar esta célula também.
   • Se você analisou todas as linhas e não eliminou a célula, não faça nada.
4. Repita o (3) até que todas as células tenham sido analisadas.

Note que este processo é exaustivo. Para não correr o risco de analisar a mesma célula várias vezes, aconselho começar pela célula mais a direita inferior e depois passar para a segunda mais a direita inferior, e assim por diante. Não faz diferença a ordem em que você analisa as células, mas você deve se organizar para não repetir células.

Durante a análise, pode acontecer de você eliminar uma linha inteira ou uma coluna inteira. Isso significa que o estado daquela linha ou coluna não é equivalente a nenhum outro estado, portanto você deve eliminar todas as células que tem alguma linha referenciando aquele estado. E.g. se você eliminou a linha toda do S3, você deve eliminar todas as células que possuam ao menos um 3 em alguma linha (x-3 ou 3-x).

Você não precisa analisar células onde todas as linhas tenham sido riscadas no passo 1. Se você riscar todas as linhas de uma célula, os estados desta célula (linha-coluna) são automaticamente equivalentes. Você não precisa tomar nenhuma ação em relação a isso, apenas pule a análise da célula.

Quando você terminar este processo, as células que você não eliminou representam classes de equivalência. Uma classe de equivalência é um grupo de estados que são equivalentes e, consequentemente, podem ser representados por um único estado. E.g. se a célula da linha 3 coluna 4 não foi eliminada, os estados S3 e S4 são equivalentes.

Exemplo 1/3 - Moore simples

Este exemplo é de uma máquina de Moore que detecta uma paridade ímpar considerando todas as entradas que já passaram pela máquina. O diagrama e a tabela de transição de estados podem ser vistos abaixo:

Tabela E1
E.A.	P.E.
	0	1
A/0	A	B
B/1	B	C
C/0	C	B

Tente minimizar esta máquina usando o método de análise da tabela de transição. É possível encontrar algum estado equivalente? Perceba que os estados A e C são equivalentes, mas não é possível perceber isto apenas com a tabela de transição de estados.

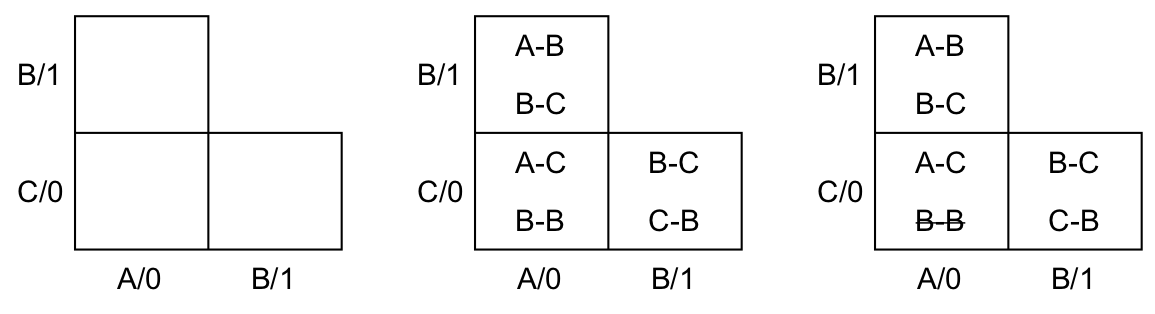Vamos construir a tabela de implicação para verificar. Na figura ao lado, podemos ver: (esquerda) a tabela de implicação construída e com os estados (note que é uma máquina de Moore, então as saídas são representadas nos estados); (meio) a tabela de implicação com as linhas de acordo com a tabela de transição de estados; e (direita) a versão com a linha B-B já riscada, pois para esta entrada, a máquina transiciona para o mesmo estado independententemente de qual estado esteja. Isto equivale à construção da tabela de implicação e à execução do primeiro passo do algoritmo.

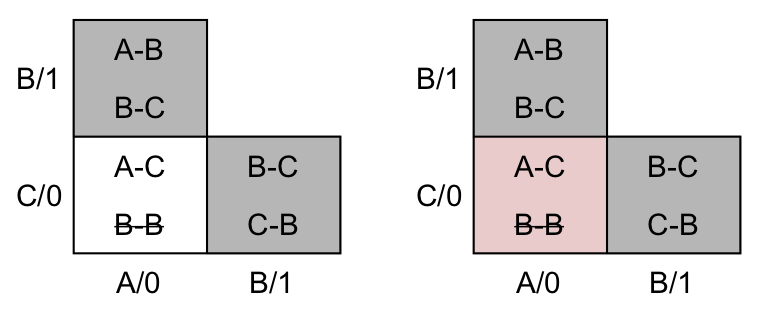No segundo passo eliminamos os estados que produzem saída diferentes, pois nunca poderão ser equivalentes. Isto pode ser visto à esquerda na figura ao lado (os estados eliminados foram destacados em cinza). Sobra a única célula a ser verificada, correspondente aos estados C/0-A/0. Esta célula tem uma linha riscada (que não precisa ser analisada) e uma linha que referencia A-C. A referência A-C aponta para a mesma célula que estamos analisando, a célula C/0-A/0. Como esta célula ainda não foi eliminada, nada resta a fazer e devemos continuar o algoritmo. Porém, não há mais células a serem analisadas, portanto o algoritmo terminou. Isso significa que a única célula que não foi eliminada será a nossa classe de equivalência, destacada em vermelho na tabela de implicação da figura.

A célula indica que a classe de equivalência contém somente dois estados, o C/0 e o A/0. Para finalizar, montamos um novo diagrama de transição de estados com um estado chamado AC/0, em vermelho, representando a classe de equivalência encontrada. As transições são transportadas dos estados da classe de equivalência e, obviamente, são esperadas que sejam as mesmas pois os estados são equivalentes. Esta máquina tem a mesma funcionalidade que a anterior, porém tem um estado a menos. Este tipo de minimização não é possível usando a análise da tabela de transição de estados.

Exemplo 2/3 - Moore com entrada de 2 bits

A Tabela E2 é a tabela de transição de estados de uma máquina de Moore, com entrada de dois bits. Sua funcionalidade ou diagrama de transição de estados não importam neste momento, mas o diagrama equivalente pode ser visto na figura.

Tabela E2
E.A.	P.E.
	00	01	10	11
S0/1	S0	S1	S2	S3
S1/0	S0	S3	S1	S5
S2/1	S1	S3	S2	S4
S3/0	S1	S0	S4	S5
S4/1	S0	S1	S2	S5
S5/0	S1	S4	S0	S5

Nas tabelas abaixo podemos ver a tabela construída e com o passo 1 executado (esquerda) e após o passo 2 executado (direita). Note que, para minimizar o esforço em preencher a tabela e evitar poluí-la, eu eliminei o "S" e utilizei somente os índices dos estados.

Nas tabelas abaixo, podemos ver a tabela de implicação após o passo 3 executado a exaustão (esquerda) e com as classes de equivalência construídas (direita). Na tabela da esquerda, as linhas que provocaram a exclusão da tabela foram realçadas com um cinza escuro.

Pela tabela, podemos inferir que os estados S4 e S0 (Sa) são equivalentes entre si, assim como os estados S5 e S3 (Sb). A tabela de transição de estados minimizada e o diagrama de transição de estados minimizado podem ser vistos abaixo. A máquina original possuía 6 estados, o que exige 3 flip-flops para sua implementação, mas a minimizada tem 4 estados, o que exige 2 flip-flops, portanto economizamos um flip-flop apenas minimizando a máquina.

Tabela E2 min
E.A.	P.E.
	00	01	10	11
Sa/1	Sa	S1	S2	Sb
S1/0	Sa	Sb	S1	Sb
S2/1	S1	Sb	S2	Sa
Sb/0	S1	Sa	Sa	Sb

Exemplo 3/3 - Mealy com 15 estados

Suponha a mesma máquina de estados usada como exemplo no método de análise da tabela de transição de estados, mostrada na figura. Trata-se de uma máquina de Mealy que reconhece 0011 ou 1001 sem sobreposição.

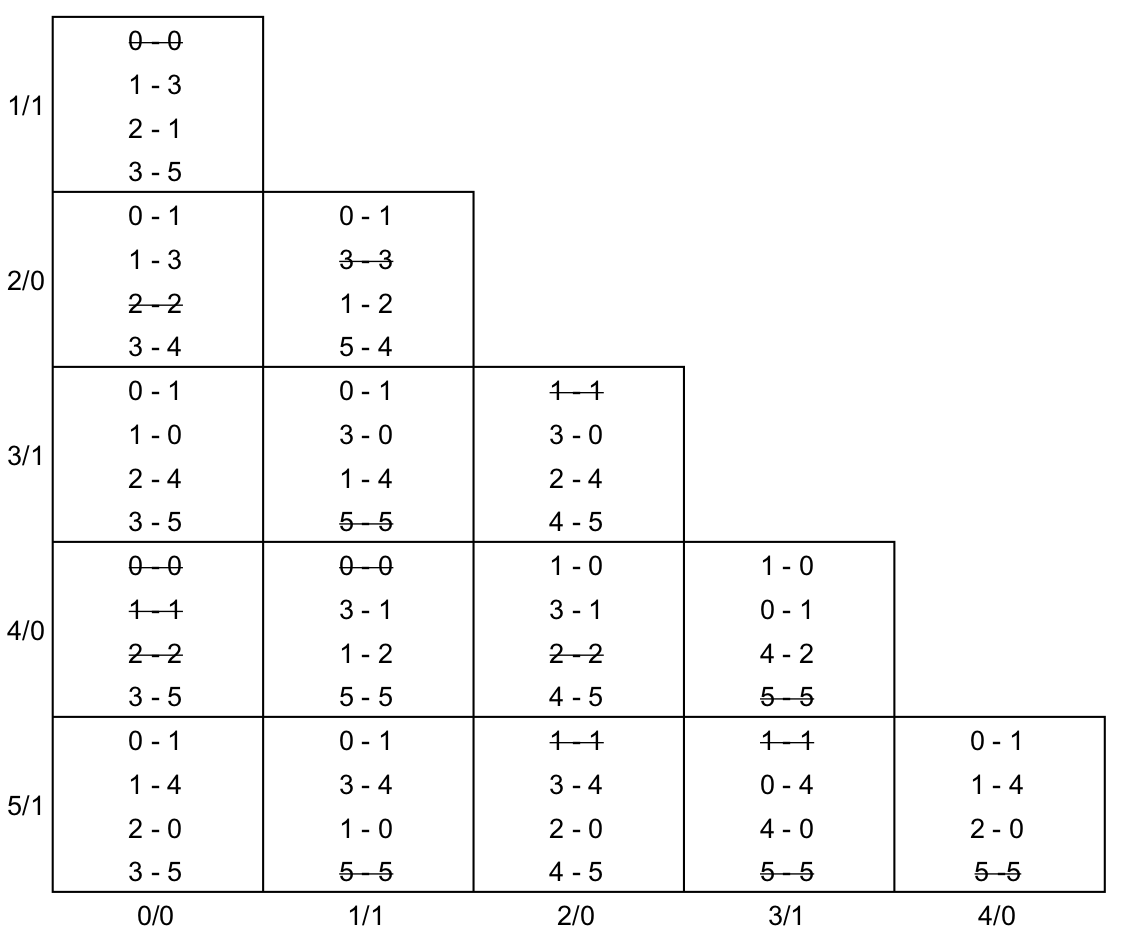
A máquina tem 15 estados, portanto temos uma matriz 15x15. A tabela de implicação, já com os valores das transições preenchidos e com as transições s-s riscadas, pode ser vista na figura abaixo. Note que esta é uma máquina de Mealy, então coloquei a saída na transição (e.g. nos estados S8 e S11, que são os que produzem saída, há transições na forma 0/1, indicando que esta transição produz saída 1). Isto corresponde à construção da tabela de implicação e à execução do passo 1 do algoritmo.

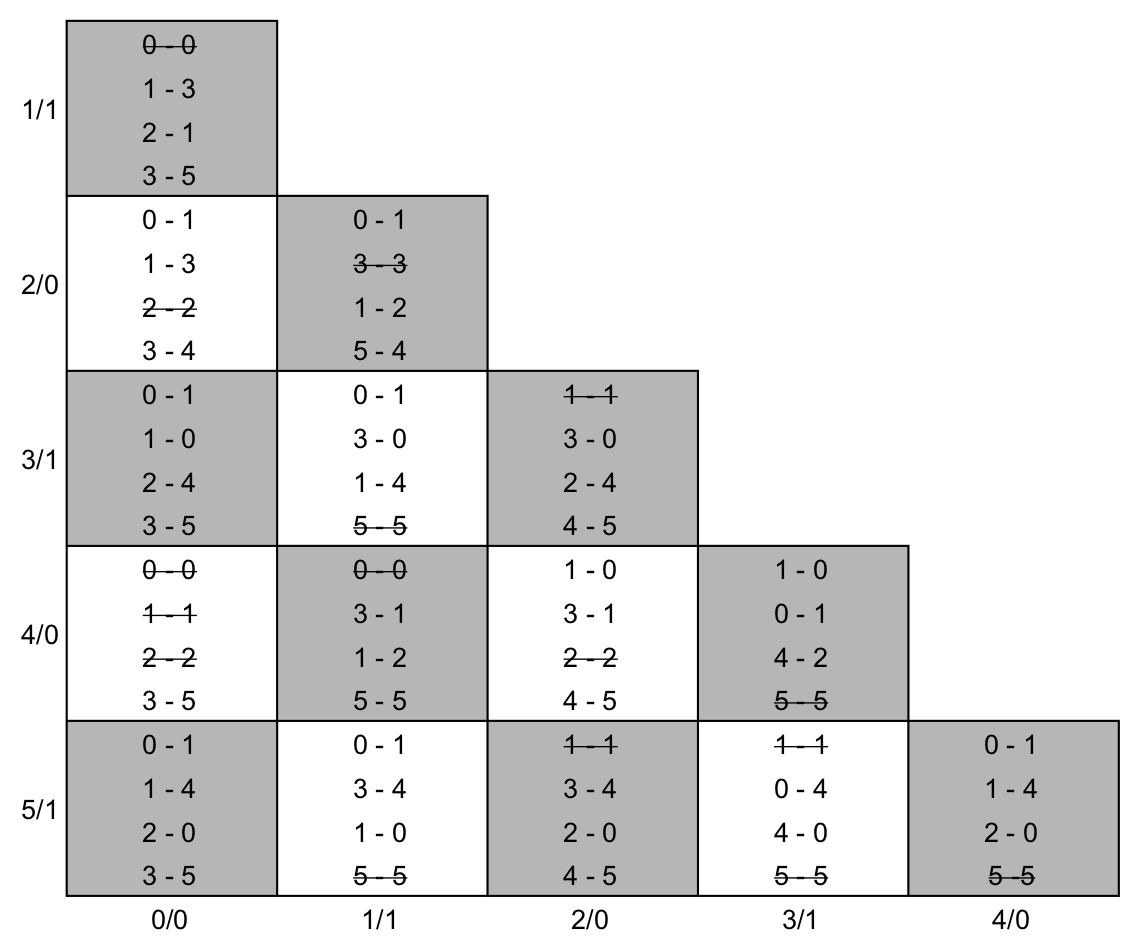
No passo 2, devemos eliminar as transições que produzem saídas diferentes, ou seja, devemos eliminar todas as células que contém uma transição s-t onde a saída de s é diferente da saída de t. Exemplo: a célula S14-S11 possui a segunda linha como 0/1-0, o que significa que, apesar de irem para o mesmo estado, uma produz saída 1 (0/1) e outra produz saída 0 (0/0), portanto devemos eliminar esta célula toda. Isto pode ser visto na figura abaixo, onde todas as células eliminadas por este motivo foram identificadas com fundo cinza e a linha que foi o motivo da eliminação com cinza escuro.

O passo 2 eliminou os estados que trivialmente não são equivalentes. Podemos então começar o passo 3 analisando cada célula. Eu comecei pela célula mais a direita inferior e continuei analisando para a esquerda. A célula S14-S13 não precisa ser analisada pois tem todas as transições riscadas. Idem para a célula S14-S12. Já a célula S14-S11 foi eliminada anteriormente e também não precisa ser analisada.

A primeira célula que realmente precisa ser analisada é a S14-S6. Nesta célula, a transição 13-0 aponta para a a célula S13-S0, e a transição 14-0 para a célula S14-S0. Estas células alvo ainda indicam equivalência, então não fiz nada na célula em análise (S14-S6). Idem para S14-S5 e S14-S4.

Já na célula S14-S3, encontrei uma referência à S8-S0, que já foi eliminado em um passo anterior. Isso significa que eu devo eliminar esta célula. Nesse ponto, percebi que a linha do S8 estava inteira eliminada, então eliminei todas as células que fazem referência a S8, ou seja, que tem transições 8/x-x/x ou x/x-8/x. O resultado pode ser visto na figura abaixo.

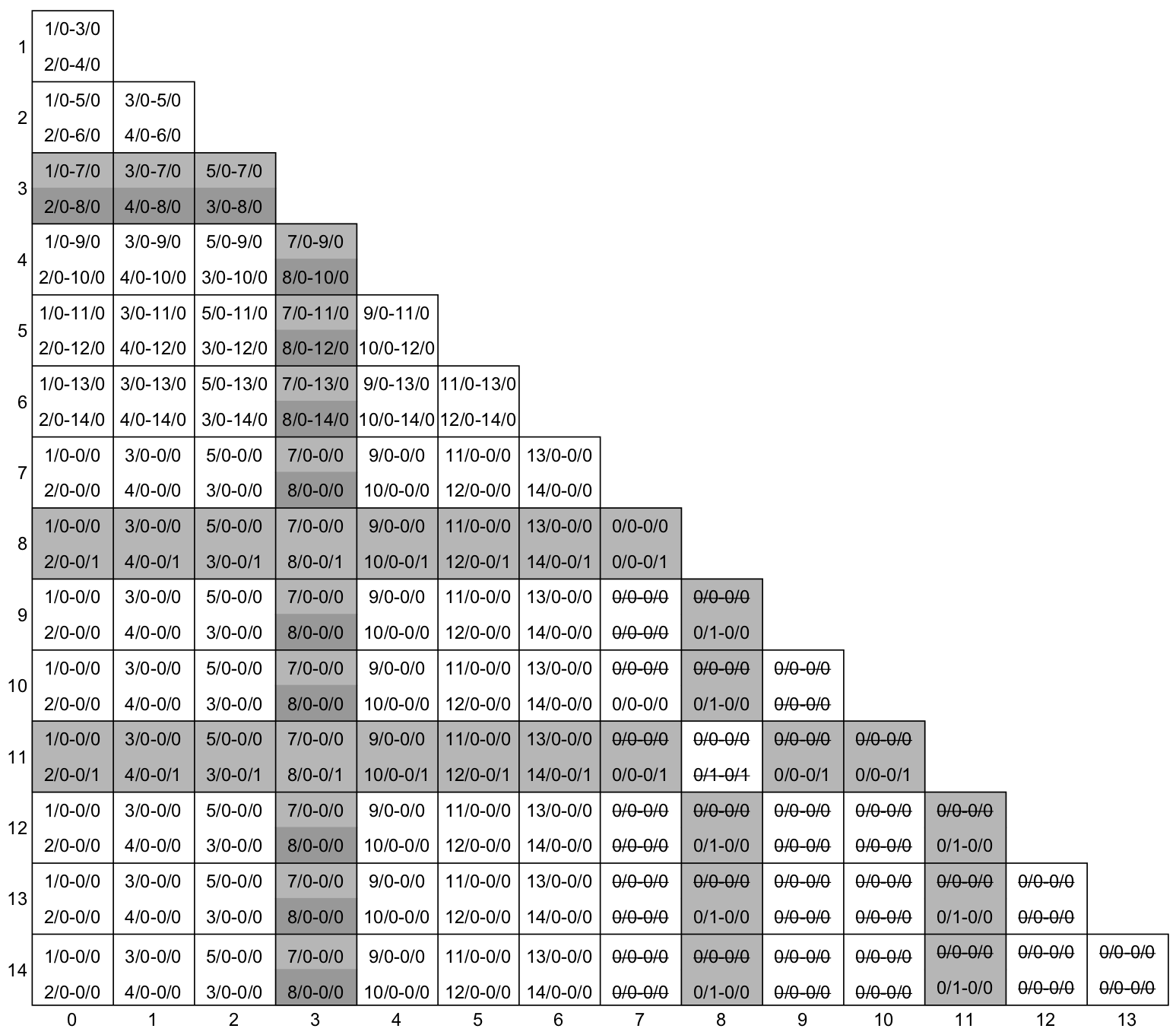
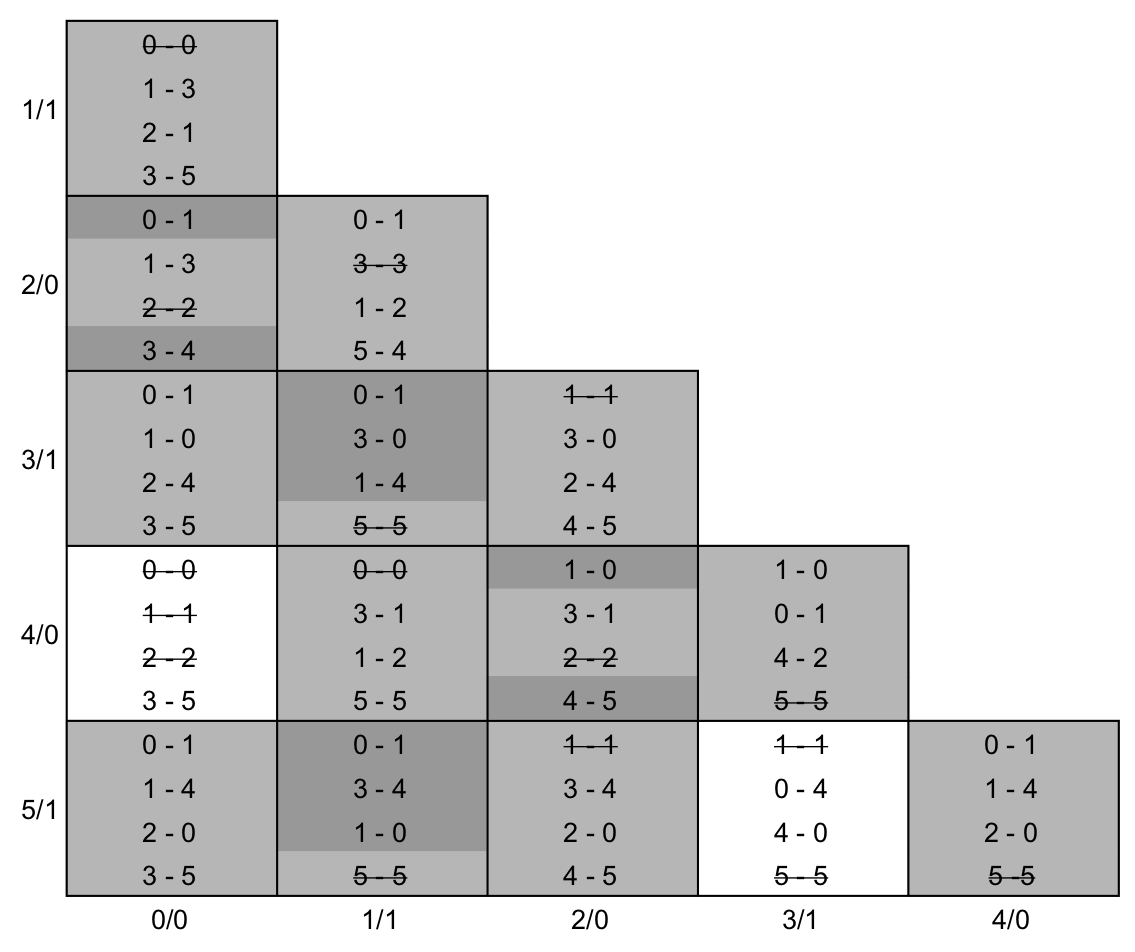
Se está lendo com cuidado, deve ter percebido que a eliminação que acabei de fazer eliminou o estado S3 inteiro. Isto significa que podemos eliminar todas as células que contém transições que referenciam o S3, pois ele não pode ser equivalente a nenhum outro estado. Se você continuar o algoritmo, terminará com a tabela de implicação abaixo, onde as células eliminadas estão em cinza.

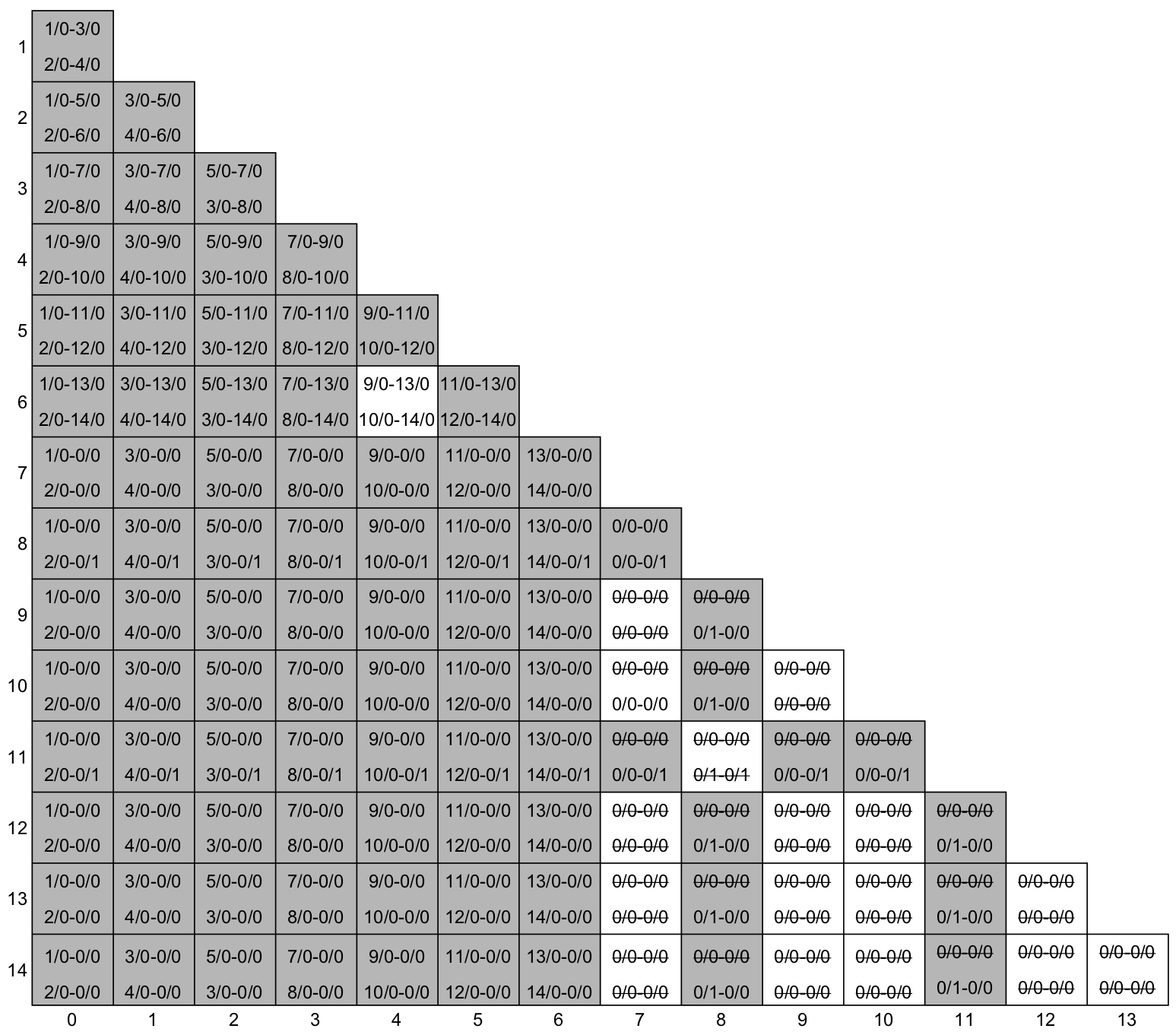
A única célula que ainda precisa de análise é a célula S6-S4. Esta célula referencia os estados S9-S13 na primeira linha e S10-S14 na segunda linha. Ambas as células S9-S13 e S10-S14 não foram eliminadas pois possuem todas as suas linhas riscadas, então não devemos fazer nada nesta célula. Como não há mais células a serem analisadas, o algoritmo terminou.

Com o algoritmo finalizado, podemos inferir os estados equivalentes observando as células que não foram eliminadas. A célula S6-S4 indica que estes dois estados são equivalentes. Similarmente, a coluna S7 indica que os estados S7, S9, S10, S12, S13 e S14 são todos equivalentes. Isso pode ser corroborado pelas colunas do S9, S10, S11, S12 e S13, que indicam também esta equivalência. Ainda, a célula S11-S8 indica que estes dois estados são equivalentes entre si (note que ambos produzem saída 1).

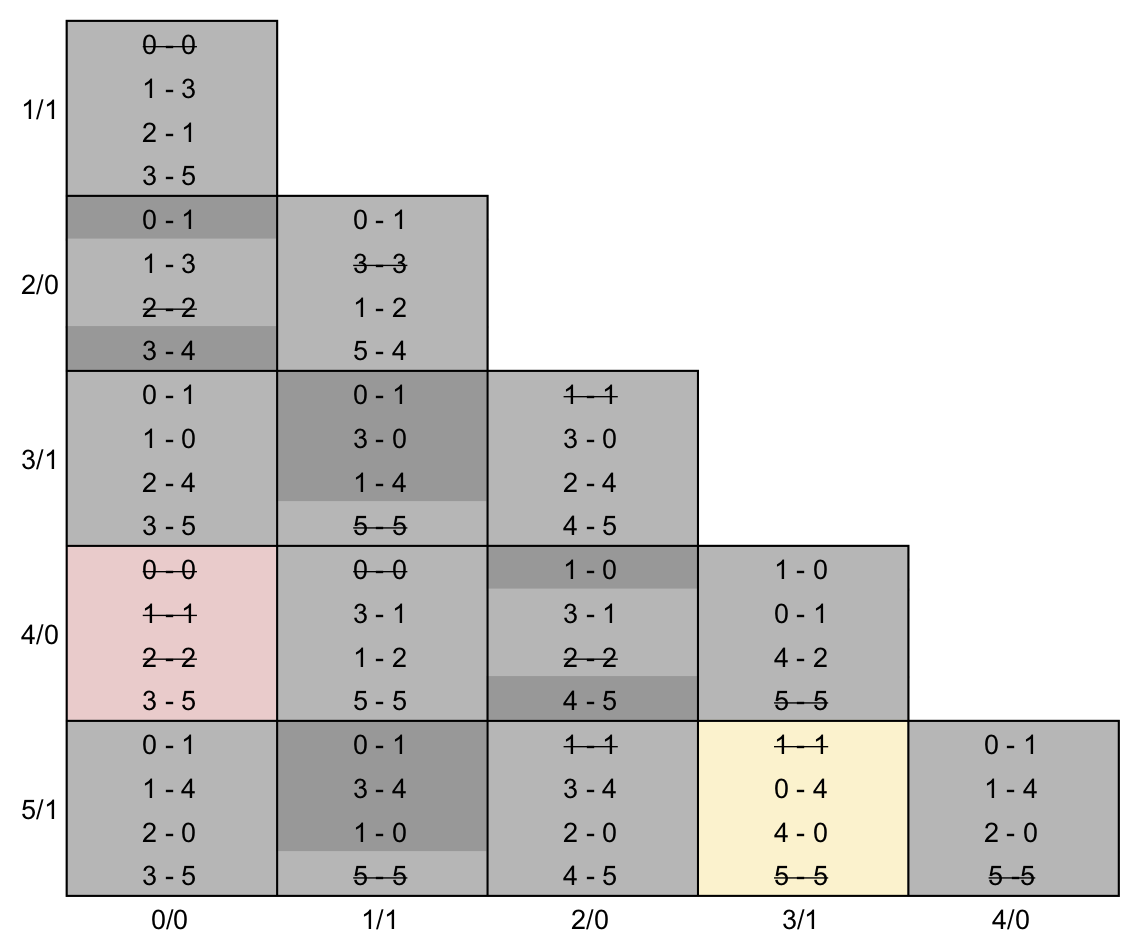
Para facilitar a visualização, a figura abaixo traz as classes de equivalência coloridas. Para a mesma cor, os estados são equivalentes.

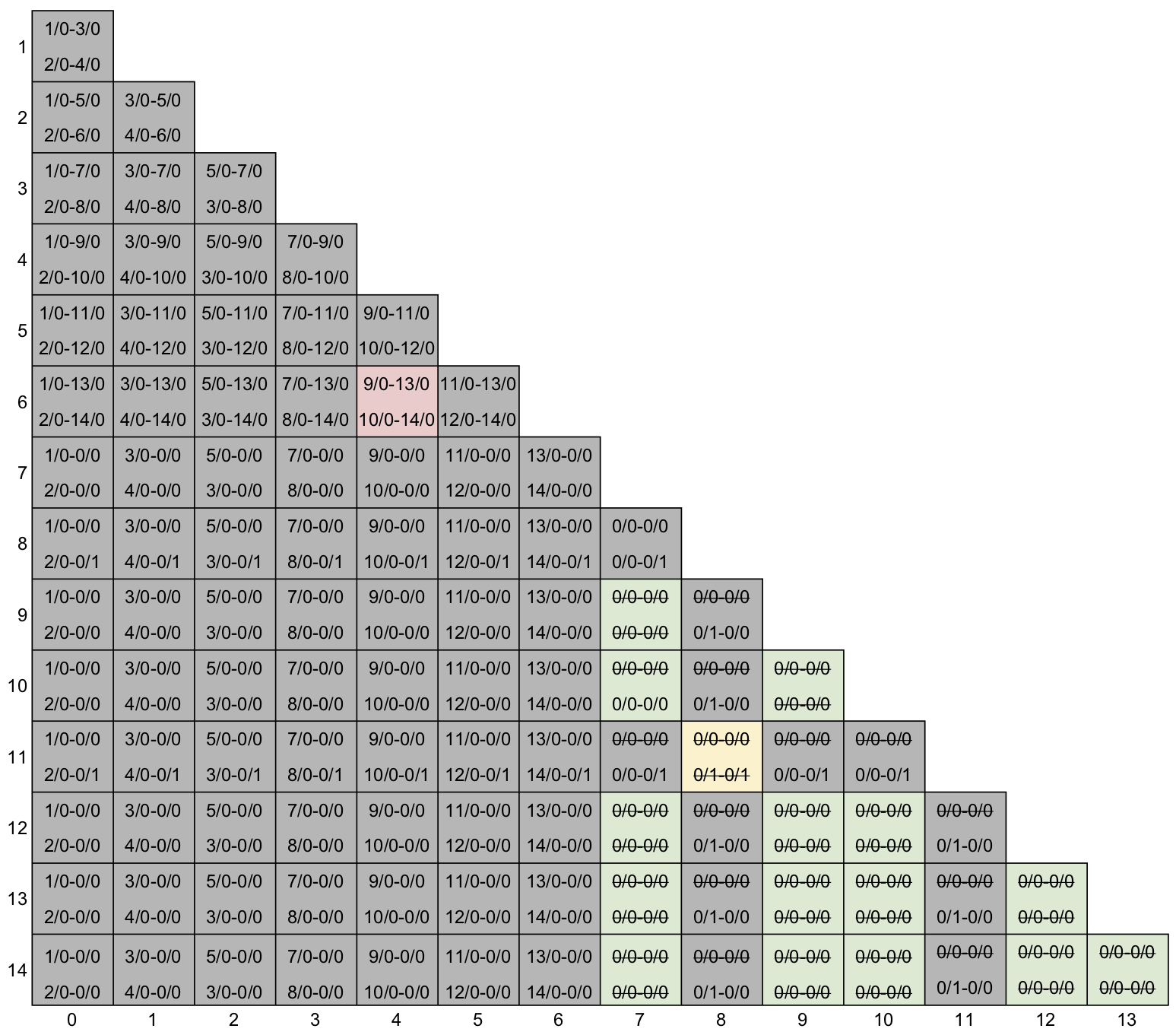
Por último, devemos reconstruir o diagrama de transição de estados. Para cada classe de equivalência, criamos um estado novo. As transições e as saídas podem ser copiadas de qualquer um dos estados da classe, pois eles são equivalentes (para as mesmas entradas, produzem a mesma saída e transicionam para o mesmo estado). Note que este método agrupa os estados em classes, então a transição do Sb (que é composto por S4 e S6) que vai para o S9, por exemplo, deve ir para o estado Sa (que é composto por S7, S9, S10, S12, S13 e S14) pois esta é a classe de equivalência que contém o S9. O diagrama desta tabela é idêntico ao obtido usando o método de análise da tabela de transição de estados.

Referências

[1] DE VRIES, A. Finite automata: Behavior and synthesis. Elsevier, 2014.
[2] KAM, Timothy et al. Synthesis of finite state machines: functional optimization. Springer Science & Business Media, 2013.

Algumas partes dos exemplos foram adaptados de apresentações do Prof. Randy H. Katz e da disciplina CSE370, Lecture 22.