Uma máquina de estados é uma representação matemática de um sistema dependente de tempo. É composta por estados e transições. Cada estado representa o sistema em um determinado momento no tempo e não é possível uma máquina de estados estar em dois estados ao mesmo tempo. Quando uma máquina está em um estado, ela aguarda que as condições para uma transição sejam atingidas e, assim que forem, muda para o estado indicado por esta transição, repetindo o ciclo o ciclo. Cada máquina possui um estado inicial, onde a máquina começa, e pode ter um ou mais estados finais (ou de aceitação), indicando que a máquina terminou a tarefa computacional. É um modelo de computação bastante utilizado para modelar circuitos sequenciais.

Tecnicamente, a máquina de estados finita que estudamos em sistemas digitais é um transdutor de estados finitos. A diferença primária entre uma máquina de estados e o transdutor é que este último não tem um estado de aceitação.

Uma máquina de estados finita pode ser especificada por uma sêxtupla do tipo: $$ M=(S, S_0, \Sigma, \Lambda, T, G) $$ Onde $S$ é o conjunto de estados possíveis e $S_0$ é o estado inicial, $\Sigma$ e $\Lambda$ denotam os alfabetos da máquina, respectivamente de entrada e de saída, $T$ é a função de transição de estados e $G$ a função de saída.

As funções de transição de estados e de saída são dadas por $T:S\times\Sigma\rightarrow S$ e $G:S\rightarrow\Lambda$ (Moore) ou $G:S\times\Sigma\rightarrow\Lambda$ (Mealy).

É importante notar que o alfabeto de entrada e saída em sistemas digitais é sempre ${0,1}$ pois, quando o circuito for realizado, todos os sinais da máquina serão binários. Isso significa que $\Sigma=\Lambda$, então alguns autores simplificam a máquina de estados para uma quíntupla: $$ M=(S, S_0, \Sigma, T, G) $$

Outra diferença notável das máquinas de estado finitas em sistemas digitais em relação ao conceito matemático é o determinismo. Em sistemas digitais, as máquinas podem ter transições aceitando $\epsilon$, ou seja, transições que acontecem independentemente da entrada, mas não podem ter mais de uma transição para a mesma entrada. Isso significa que as implementações de máquinas de estados finitas em sistemas digitais são sempre determinísticas.

Conceito de máquina de estados finita em sistemas digitais

Já afirmamos que a máquina de estados em sistemas digitais não tem um estado de aceitação. Isso significa que a máquina é infinita, ou seja, executa para sempre. O modelo de estado de aceitação pode ser facilmente implementado colocando uma transição para o próprio estado (laço) e fazendo com que este estado produza uma saída pertinente à tarefa cuja máquina deveria realizar.

Em sistemas digitais, a máquina de estados representa um circuito sequencial. Quando síncrono, há uma transição de estados em cada borda de clock (normalmente especifica-se somente uma das bordas, e.g. borda de subida). A transição pode ser para o mesmo estado (laço) ou vazia (incondicional), mas sempre ocorre na borda do clock. Quando assíncrona, a transição ocorre assim que uma das condições para transição é satisfeita, portanto não é aconselhável especificar transições vazias neste tipo de máquina.

Como a máquina é determinística, em cada estado deve haver transições contemplando cada combinação possível de entrada.

Revisitando a quíntupla $M=(S, S_0, \Sigma, T, G)$, podemos fazer algumas considerações sobre sua aplicação em sistemas digitais. $S_0$ é o estado que a máquina deve assumir inicialmente, portanto deve ser o estado da máquina após um reset. Normalmente o reset das máquinas de estados é assíncrono e ativo baixo por motivos históricos ligados a implementação, mas não há impedimentos para adotar-se outras abordagens, desde que possa-se colocar a máquina explicitamente no estado inicial de alguma forma. O alfabeto $\Sigma$ já foi dito que é sempre o binário ${0,1}$, mas é possível existir entradas e saídas com mais de um bit. O $S$ representa o conjunto de estados possíveis e na implementação em sistemas digitais, sempre é um elemento de memória. As funções $T$ (função de excitação ou de próximo estado) e $S$ (função de saída) são circuitos combinatórios. A figura abaixo ilustra o modelo.

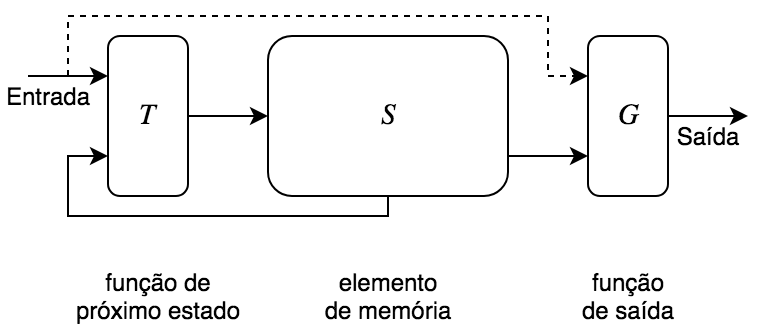
A linha pontilhada é opcional e, quando presente, indica que a máquina é uma máquia de Mealy.

Representação Gráfica

A representação gráfica de uma máquina de estados finita em sistemas digitais é o diagrama de transição de estados. Cada estado é representado por um círculo e as transições são representadas por setas. Na figura ao lado podemos ver uma máquina de estados com dois estados (A e B) e quatro transições. Nas transições estão especificadas que entradas levam a tomada daquela transição.

No caso ao lado, a máquina é de Mealy, então a transição especifica um par e/s onde e é a entrada e s é a saída. Exemplo: se estivermos no estado B e a entrada for 0, continuaremos no estado B e produziremos saída 1; já se estivermos no mesmo estado mas a entrada for 1, iremos para o estado A e produziremos saída 0. A especificação formal desta máquina é:

$$M=(S, S_0, \Sigma, T, G)\ S={A,B}\quad S_0=A\quad \Sigma={1,0}\ T={(A,0)\rightarrow A,(A,1)\rightarrow B,(B,0)\rightarrow B,(B,1)\rightarrow A}\ G={(A,0)\rightarrow 0,(A,1)\rightarrow 1,(B,0)\rightarrow 1,(B,1)\rightarrow 0}$$

Uma máquina de Moore pode é representada da mesma forma, porém o círculo representando o estado é cortado ao meio e a saída é especificada na parte inferior, como na figura ao lado. As transições, representadas pelas arestas, possuem somente a entrada e especificada, pois nesta máquina a saída não depende da entrada e sim somente do estado.

A especificação formal é similar, porém a função de de saída ($G$) não possui a entrada:

$$M=(S, S_0, \Sigma, T, G)\ S={A,B}\quad S_0=A\quad \Sigma={1,0}\ T={(A,0)\rightarrow A,(A,1)\rightarrow B,(B,0)\rightarrow B,(B,1)\rightarrow A}\ G={A\rightarrow 0,B\rightarrow 1}$$

Síntese

Dado que $S$ é um elemento de memória, podemos usar qualquer um dos elementos de memória disponíveis para implementá-lo. É comum a utilização de flip-flops, mas até mesmo memórias capacitivas podem ser utilizadas. Já as funções de transição de estados (também chamada de função de próximo estado ou de excitação) e de saída, por serem circuitos combinatórios, são sintetizadas como tal. Pode-se usar qualquer técnica de síntese de circuitos combinatórios para ajudar, desde álgebra booleana até mapas de Karnaugh. O mais comum é montar uma tabela verdade com os estados e depois sintetizar usando-se minimização por Karnaugh e desenho direto das equações em forma de diagrama esquemático.

Os passos para a síntese de uma máquina de estados finita em sistemas digitais são:

1. Entender o problema (enunciado, texto, variáveis de entrada e saída, temporização, etc.);
2. Elaborar uma descrição funcional da máquina;
   • Elaborar um diagrama de transição de estados;
3. Obter a tabela de estados e a tabela de saídas;
   • Reduzir as tabelas;
4. Designação de estados;
5. Tabela de excitação;
6. Projeto dos circuitos combinatórios (funções $T$ e $G$);
7. Montagem do diagrama lógico (esquemático).

O passo 1 consiste em entender o comportamento do sistema sequencial sendo modelado. Em muitos casos o diagrama esquemático está disponível, simplificando este passo. Em outras palavras, é possível sintetizar uma máquina de estados sem o conhecimento da aplicação, desde que o passo 1 ou o passo 2 estejam disponíveis. Neste passo, você deve identificar todas as entradas e saídas da máquina de estados, assim como o momento exato onde cada saída deve ser gerada. Se for necessário, faça uma carta de tempos do funcionamento da máquina. Neste passo também devemos escolher se usaremos o modelo de Melay ou de Moore.

No passo 2 devemos identificar o número de estados necessários e anotar os momentos em que as saídas serão produzidas. A forma mais comum é expressar a saída deste passo com um diagrama de transição de estados. Pode ser útil nomear os estados no final do desenho do diagrama, pois este tende a mudar conforme se exercita a máquina. O teste de mesa (exercitar a máquina com entradas), é crucial para termos certeza que o diagrama atende a solução do problema. Também não precisamos nos preocupar com estados excessivos ou redundantes pois a máquina será minimizada posteriormente.

A tabela de estados e a tabela de saída costumam ser montadas juntas, no passo 3. Esta tabela tem as mesmas informações que o passo 2, porém em forma de tabela. Opcionalmente podemos minimizar as tabelas usando um método de minimização de máquinas de estado.

Com as tabelas minimizadas, o passo 4 visa qualificar e quantificar o elemento de memória a ser usado ($S$). Normalmente usamos $n$ flip-flops tipo D, sendo $n=\lceil log_2s\rceil$, onde $s$ é o número de estados. Caso o número de estados não seja uma potência de 2, deve-se decidir neste passo o que fazer com os estados que sobrarem. As opções possíveis são: (i) nada, assim aumentamos as possibilidades de minimização das funções combinatórias mas caso a máquina alcance um destes estados, a saída pode não ser neutra; (ii) forçar a saída para um valor neutro, diminuindo as possibilidades de minimização da função de saída; ou (iii) idem ao (ii) mas também forçamos a máquina para o estado inicial no próximo ciclo. A opção (i) é a que oferece a maior possibilidade de minimização e a opção (iii) é a mais segura. Com as escolhas feitas, deve-se determinar as variáveis de estado e designar o código de cada estado. Uma boa designação de estados pode implicar em melhor minimização, mas não há uma regra específica. Um truque comum é designarmos os estados usando código de Gray, assim os mapas de Karnaugh podem ser facilmente montados (assumindo que você utilizará esta técnica).

Caso não tenha escolhido o tipo de flip-flop no passo 4, você deve escolher antes de começar o passo 5. Neste passo, devemos montar a tabela de excitação levando em consideração as características do elemento de memória escolhido. O nome desta tabela (tabela de excitação) remete às informações da tabela, pois esta não traz o próximo estado e sim o que deve ser colocado nas entradas dos elementos de memória para que suas saídas sejam o próximo estado no momento adequado (i.e. próxima borda do clock).

Temos a tabela de excitação (passo 5) e a tabela de saída (passo 3), com a designação de estados e as variáveis de estado (passo 4). No passo 6 devemos encontrar as funções de chaveamento. A técnica usual é montar os mapas de Karnaugh para a função de excitação ($T$) e para a função de saída ($G$), obtendo as equações como produto da aplicação do mapa. No entanto, qualquer técnica de síntese de circuitos combinatórios pode ser utilizada.

Com as equações prontas, basta desenhar os blocos combinatórios ($T$ e $G$), posteriormente ligando-os aos elementos de memória e obtendo-se o circuito final, o que é feito no passo 7.

Análise

A análise de uma máquina de estados finita em sistemas digitais é exatamente o contrário da síntese.

Parte-se de um diagrama lógico (passo 7 reverso), onde deve-se identificar o elemento de memória ($S$). É comum o elemento de memória ser composto por um ou mais flip-flops, então não é difícil encontrá-los no circuito.

Identificado o elemento de memória, segue-se a identificação das funções de excitação e de saída (passo 6 reverso). Isso pode ser feito usando uma técnica de análise de circuitos combinatórios, partindo da saída do elemento de memória em direção ao que se pretende identificar (e.g. se você está identificando a função de saída, aplique uma técnica de análise da saída do elemento de memória em direção a saída da máquina de estados). É útil ter em mente o modelo clássico de máquinas de estado pois, identificado o elemento de memória, o que sobrou deve ser combinatório e faz parte de uma das funções de excitação ou saída. É muito comum usar cores, circular ou marcar as portas lógicas para separá-las de acordo com a função conforme se faz a análise. Neste ponto da análise já é possível identificar se a máquina segue o modelo de Moore ou de Mealy. Neste passo deve-se também inferir as variáveis de estado (no caso dos flip-flops as variáveis de estado coincidem com a saída dos mesmos).

Obtidas as equações $T$ e $G$, parte-se para as tabelas. A tabela de excitação pode ser obtida exercitando todas as combinações possíveis das variáveis de estado e das entradas (passo 5 reverso). Para cada valor, exercita-se a função de excitação ($T$) e obtém-se o valor que será aplicado às entradas do elemento de memória ($S$).

Com a tabela de excitação e conhecendo-se as características do elemento de memória, pode-se atribuir nomes aos estados e construir a tabela de transição de estados (passo 4 reverso). É difícil atribuir nomes significativos para o estado neste momento, então muitos projetistas optam por atribuir nomes alfanuméricos (e.g. A, B, C1, C2, etc).

Não faz sentido reverter as minimizações, tanto para os métodos de síntese combinatória quanto para as tabelas, portanto das equações montamos diretamente as tabelas, e delas extrairemos diretamente o restante.

Para completar as tabelas (passo 3 reverso), obtemos a tabela de saída a partir da função de saída (encontrada no passo 6 reverso) da mesma maneira que encontramos a função de excitação: exercitando todos os valores possíveis para as variáveis de estado e para a entrada (a entrada só faz parte da função de saída se a máquina seguir o modelo de Mealy).

Com as tabelas, é possível montar um diagrama de transição de estados. O diagrama pode ser inferido diretamente das tabelas (passo 2 reverso).

O passo 1 é o único críptico na análise de máquinas de estado finitas. A razão disso é que o diagrama pode ser considerado a expressão de uma solução para um problema. Extrair o problema de uma solução é uma tarefa subjetiva. Informações extras sobre a aplicação da máquina, o local onde ela funciona, interfaces e até mesmo observar os sistemas ao redor da máquina de estados podem ajudar, porém não há uma técnica para este passo. Em alguns casos pode-se tentar mapear a máquina de estados para uma estrutura formal (e.g. expressões regulares), mas isso pouco ajuda quando não se conhece nem mesmo a natureza do problema que a máquina resolve.

Exemplo

Este é um exemplo clássico de uma máquina de estados simples, mas que todos reconhecem: o semáforo. Projete o circuito para uma máquina de estados que opere um semáforo de três fases: verde, amarela e vermelha. A entrada é $m$, proveniente de um temporizador, que caso alta na fase verde causa uma mudança para a fase a amarela e caso alta na fase vermelha causa uma mudança para a fase verde. A mudança da fase amarela para a vermelha é independente da entrada. A saída da máquina de estados é dada por dois bits, $c_1c_0$, que indicam qual cor está acesa: 10 verde, 11 amarelo e 01 vermelho.

Passo 1: Variáveis de entrada: somente $m$ de 1 bit. Variáveis de saída: $c_1c_0$ de 2 bits, 10 verde, 11 amarelo e 01 vermelho (não foi especificado o que acontece em 00). O semáforo trabalha de forma circular acendendo as cores vermelho, amarelo e verde, em sequência repetitiva. O tempo que a máquina permanece na cor amarela é dado pelo período do clock, pois não há condição para a transição. Já o tempo que a máquina permanece no vermelho e no verde é indicado pelo sinal do temporizador, representado pela entrada $m$. Quando a entrada for alta ($m=1$), deve-se trocar de estado na próxima borda do clock. Convencionaremos o reset assíncrono ativo baixo e o elemento de memória sensível a borda de subida do clock. Escolheremos um modelo de Moore, sem nenhuma vantagem ou desvantagem explícita.

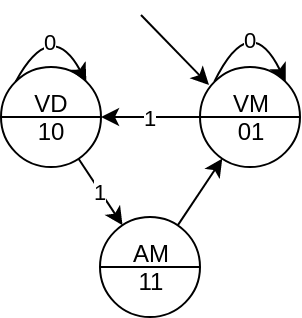Passo 2: A descrição funcional foi feita durante a análise do problema no passo 1. O diagrama de transição de estados pode ser visto na figura ao lado. Note que já demos os nomes para os estados de acordo com a cor: VM vermelha, VD verde e AM amarela. A entrada de 1 bit foi especificada nas transições e a saída de 2 bits na parte inferior do estado, de acordo com o identificado no passo 1.

Passo 3: Já temos o diagrama de transição de estados, então podemos montar as tabelas.

Estado Atual	Próximo Estado		Saída
	m=0	m=1
VM	VM	VD	01
AM	VM	VM	11
VD	VD	AM	10

Note que as tabelas de próximo estado e de saída estão juntas na mesma tabela. A coluna Estado Atual mostra o estado em que a máquina se encontra, e a coluna Saída mostra a saída para aquele estado. A coluna Próximo Estado contém as transições, ou seja, para qual estado a máquina irá no próximo ciclo de clock caso a entrada $m$ seja 0 ou 1. Esta tabela é pequena, portanto basta uma rápida análise para perceber que não há reduções possíveis.

Dica: é muito comum representar as duas tabelas em uma só para economizar espaço, pois a coluna de estado atual é idêntica nas duas. Note também que a ordem dos estados já foi colocada de forma a facilitar a utilização do método de minimização gráfica por mapa de Karnaugh.

Passo 4: Para nossa implementação, usaremos flip-flops tipo D sensíveis a borda de subida do clock. Temos 3 estados, portanto usaremos $\lceil log_23\rceil =2$ flip-flops. Com dois flip-flops, podemos representar até $2^2=4$ estados possíveis, portanto há um estado sobrando. A aplicação é crítica pois caso a máquina atinja o estado AM ou VD erroneamente, poderá causar um acidente. Neste sentido, optamos por forçar o estado extra para produzir uma saída vermelha (10) e ir para o estado VM no próximo ciclo, independente da entrada. A designação de estados será: 00 para o estado extra, que chamaremos de EX; 01 para o estado VM, 11 para o estado AM, e 10 para o estado VD. Note que esta designação condiz com a saída para os estados válidos, o que foi proposital para minimizar as funções de saída.

Passo 5: A tabela de excitação é exatamente a tabela de próximo estado, porém com os estados substituídos pela sua designação pois usamos flip-flops tipo D, que copiam a entrada para a saída. Caso o elemento de memória fosse diferente, nesta tabela deveríamos colocar as entradas do elemento de memória adequadas para que o próximo estado seja o ta tabela de transição de estados. Também copiamos a tabela de saída para incluir a saída no caso do estado extra.

Estado Atual	Próximo Estado		Saída
	m=0	m=1
EX(00)	VM(01)	VM(01)	01
VM(01)	VM(01)	VD(10)	01
AM(11)	VD(01)	VD(01)	11
VD(10)	VD(10)	AM(11)	10

Mantivemos os nomes dos estados e colocamos a designação entre parênteses para facilitar a leitura (esta prática é comum quando utiliza-se flip-flop tipo D). Os números entre parênteses representam as variáveis de estado, que chamaremos de $q_1q_0$.

Passo 6: Neste passo, devemos encontrar as funções de excitação e de saída. A construção e solução do mapa de Karnaugh foi omitida pois não é assunto deste artigo, porém ambas as equações foram encontradas usando este método. Note que, como usamos flip-flops tipo D, $d_1=q_1^{t+1}$ e $d_0=q_0^{t+1}$.

$$ q_1^{t+1}=q_1.\overline{q_0}+\overline{q_1}.q_0.m\ q_0^{t+1}=\overline{q_1}.\overline{q_0}+q_0.\overline{m}+q_1.m\ \quad\ c_1=q_1\ c_0=\overline{q_1}+q_0 $$

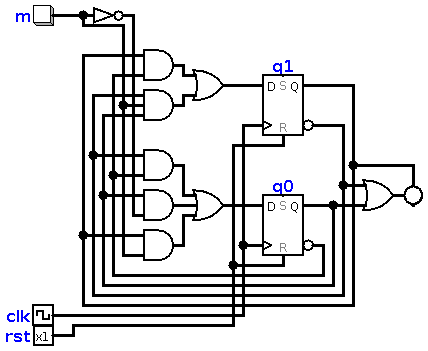Passo 7: Com as equações em mãos, basta montar o circuito correspondente. Começamos colocando os elementos de memória na parte central (dois flip-flops) tipo D e nomeamos como q1 e q0. As saídas dos flip-flops correspondem às variáveis de estado homônimas, e as entradas devem ser as saídas das funções de próximo estado. Após colocarmos os elementos de memória, continuamos seguindo as convenções e colocamos a esquerda o circuito combinatório correspondente à função de transição de estados e a direita o correspondente a de saída. Ainda no circuito vemos a entrada de clock e de reset, um botão que emula o sinal vindo do temporizador e uma saída RGB que corresponde ao semáforo.

Para baixar este circuito no formato do LogiSim clique aqui.